|
Im Folgenden wird gezeigt, wie ein elektronischer Analogrechner zur Darstellung einer dreidimensionalen Figure in Echtzeit eingesetzt werden kann, wobei die Darstellungsparameter interaktiv während der Rechnung modifiziert werden können. Das untenstehende Bild zeigt ein Bildschirmphoto der Darstellung einer solchen Figur. Durch Klicken auf das Bild wird ein etwas 3.3 MB großes Video geladen, in dem gut zu erkennen ist, dass es mit Hilfe eines elektronischen Analogrechners möglich ist, eine solche Figur beispielsweise in Echtzeit zu drehen oder in ihrer Form zu verändern. |
|

|
|
|
Eine der faszinierendsten Eigenschaften eines elektronischen Analogrechners ist nicht allein seine Fähigkeit, Differentialgleichungen und Systeme derartiger Gleichungen in atemberaubender Geschwindigkeit zu lösen sondern darüberhinaus die unerreicht hohe Interaktivit&aauml;t eines solchen Rechners, die es erlaubt, jederzeit manuell durch Eintellen von Koeffizientenpotentiometern in eine laufende Rechnung einzugreifen und die Effekte dieser Änderungen direkt zu beobachten. Vergangenes Wochenende entschloß ich mich, eine kleine Rechenschaltung zu entwickeln, mit deren Hilfe eine dreidimensionale Figur auf einem Oszilloskop dargestellt werden kann. Diese Figur sollte während ihrer Darstellung auf dem Bildschirm rotiert werden können. Hierzu wird zunächst eine repetierende Teilrechenschaltung benötigt, um die darzustellende Figur in rascher Folge neu zu berechnen und darzustellen. Ein zweites Teilprogramm wird zur Erzeugung eines sin-/cos-Signalpaares benötigt, um hiermit die eigentliche Rotation zu implementieren. Da beide Programmteile Integrierer benötigen, ist es notwendig, zwei Gruppen von Integrierern zu bilden, die voneinander unabhängig kontrolliert werden. Während eine Integrierergruppe kontinuierlich arbeitet, wird die zweite repetierend mit kurzer Integrationszeit betrieben. Dies erfordert eine externer Steuerung dieser Integrierergruppe, die mit Hilfe des Digitalteiles meiner EAI 580, die ich vom Lehrstuhl für Meß- und Regeltechnik der Universität Karlsruhe erhielt (an dieser Stelle möchte ich Herrn Böhringer und Professor Stiller für die Überlassung des Rechners ganz herzlich danken), umgesetzt wurde. Die folgenden Abschnitte beschreiben die entwickelte Rechenschaltung, mit deren Hilfe der obige Videofilm erzeugt wurde. |
|
|
Generierung eines sin-/cos-Signalpaares: Die Erzeugung eine sin-/cos-Signalpaares mit Hilfe eines elektronischen Analogrechners ist einfach und führt fast stets auf die Lösung einer Differentialgleichung der allgemeinen Form y''=-y. Die zugehörige Rechenschaltung besteht aus zwei Integrierern sowie zwei Summierern (der zweite Summierer ist lediglich notwendig, da im weiteren Verlauf der Rechnung Parabelmultiplizierer zum Einsatz gelangen).
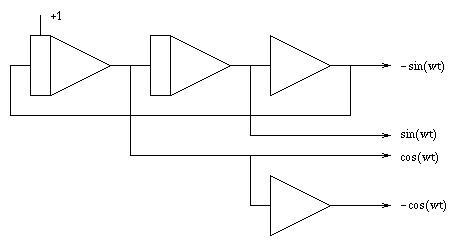
Dieser Teil des Programms wird lediglich einmal initialisiert und läft in der Folge weiter, während der andere Programmteil repetierend betrieben wird. |
|
|
Erzeugung der dreidimensionalen Figur: Um eine dreidimensionale Figur zu erzeugen, muss für jeden Punkt der Hüllfläche ein Koordinatentripel generiert werden. Ich entschied mich der Einfachheit halber, eine linear in eine dritte Dimension gestreckte Spirale als Grundfigur zu verwenden. Die unten gezeigte Rechenschaltung erzeugt die X- bzw. Y-Koordinaten einer einfachen zweidimensionalen Spirale (das Programm ist fast identisch zu dem obigen Teilprogramm und unterscheidet sich hiervon lediglich durch einen dämpfenden Term). Der Ausgabewert u(t) wird zur Ansteuerung der Y-Ablenkung des Oszilloskops verwendet, während v(t) in Verbindung mit dem oben erzeugten sin-/cos-Signalpaar und einer dritten Raumkoordinate (siehe unten) benötigt wird. Durch Ändern der Einstellung des Koeffizientenpotentiometers P1 kann die Steigung der Spirale eingestellt werden. Da diese Teilrechenschaltung in schneller Folge Spiralen erzeugt, indem getrennt gesteuerte Integrierer verwendet werden, wurden diese durch einen schwarzen Querbalken gekennzeichnet. Die Steuersignale für diese Integrierer werden mit Hilfe einer einfachen digitalen Rechenschaltung erzeugt.
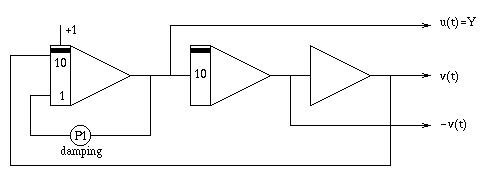
|
|
|
Die dritte Dimension: Um diese flache Spirale in eine dreidimensionale Figur zu verwandeln, wird eine dritte Variable benötigt, die linear mit der Zeit ansteigt und ebenfalls mit Hilfe eines getrennt gesteuerten, repetierend betriebenen Integrierers erzeugt wird (siehe unten).
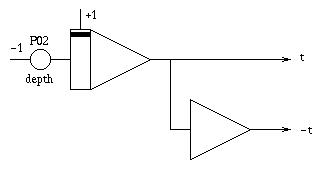
|
|
|
Die Gesamtrechenschaltung: |
|
|
Die Abbildung der durch das Koordinatentripel u(t), v(t) und t beschriebenen Figur auf ein zweidimensionales Anzeigegerät ist nun vergleichsweise einfach - benötigt werden lediglich ein niederfrequentes sin-/cos-Signalpaar sowie zwei Multiplizierer und ein Summierer:
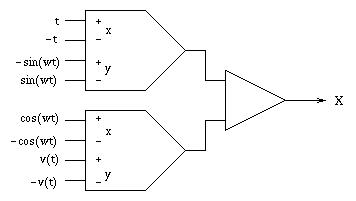
|
|

|
Die Bilder links zeigen die Gesamtrechenschaltung für den rein analogen Teil der Simulation - wie gut zu erkennen ist, wird nur ein kleiner Teil des Steckfeldes der EAI 580 von diesem Programm belegt. |
|
Steuerung der repetiv arbeitenden Integrierergruppe: Wie bereits oben beschrieben, ist es notwendig, eine Integrierergruppe unabhängig von den anderen Integrierern zu steuern, um die Koordinatentripel u(t), v(t) und t in rascher Folge zu erzeugen, um ein scheinbar stehendes, möglichst flimmerfreies Bild zu ermöglichen. Dies wird mit Hilfe einiger digitaler Schaltelemente erreicht, welche die Steuersignale RUN und IC (Anfangswert) der Integrierergruppe erzeugen. Die untenstehende Schaltung besteht aus einem einfachen UND-Gatter, das als Inverter verwendet wird sowie zwei dekadischen Zählern zur Erzeugung einer geeigneten Pulsfolge, um die drei Integrierer anzusteuern. Das mit CLK2 bezeichnete Signal wird von der EAI 580 zur Verfügung gestellt und weist eine Frequenz von 100 Hz auf.
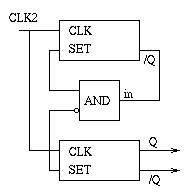
Q wird als Steuersignal IC verwendet, während sein Inverses, /Q, als RUN-Signal der Integrierergruppe dient. Bemerkenswert ist hier, dass das UND-Gatter einen Eingang, aber zwei Ausgänge besitzt - hiervon ist einer nicht invertiert, während der andere invertiert ist. Diese Signale werden benötigt, um die Zähler voreinzustellen. Der Q-Ausgang eines solchen Zählers bleibt übrigens solange 1, bis eine voreingestellte Anzahl von Taktzyklen verstrichen ist. Die beiden untenstehenden Bildern zeigen den digitalen Steuerteil der Rechenschaltung. Auf der linken Seite des digitalen Programmierfeldes kann das Signal CLK2 abgenommen werden, während die Zähler sowie das UND-Gatter auf der rechten Seite angeordnet sind. Die Verbindungen zum analogen Programmierfeld werden mit Hilfe sogenannter "Trunk-Leitungen" vorgenommen. |
|

|

|
|
Das rechte Bild zeigt den Gesamtaufbau der Rechenschaltung. Bei dem verwendeten Analogrechner handelt es sich um eine EAI 580, deren rechte Hälfte von den analogen Rechenelementen eingenommen wird, während die linke Hälfte die Bedienelemente, das Digitalvoltmeter sowie den Digitalzusatz beinhaltet. Auf dem Rechner steht das verwendete Philips Oszilloskop, das auch bei der Aufnahme des kleinen Videofilmchens zum Einsatz gelangte. |

|
|
Ich hoffe, dieser Ausflug in die Möglichkeit zur Darstellung und Manipulation mehr oder weniger komplexer Figuren in Echtzeit mit Hilfe elektronischer Analogrechner war interessant und hat Spass gemacht. Happy analog computing! :-) |
|