|
Am 19. Juli 2008 brachte mein Freund Dr. Matthias Koch ein kleines mathematisches Problem zu meiner Geburtstagsfeier mit: Gegeben sei ein Fahrzeug, das zum Zeitpunkt t=0 mit einer Initialgeschwindigkeit von 100 km/h fährt. Während seiner Fahrt verliert es kontinuierlich an Geschwindigkeit, wobei es pro gefahrenem Kilometer um 1 km/h langsamer wird. Die Frage lautet: Wie lange dauert es, mit diesem Fahrzeug eine Strecke von 50 km zurück zu legen? Zunächst ist klar, dass dv /ds = -1, da der Graph der gegen die Strecke abgetragenen Geschwindigkeit linear, mit v = 100 km/h bei s = 0 km beginnend, fällt und bei s = 100 km den Wert 0 km/h erreicht. Offensichtlich erreicht man niemals den Punkt s = 100 km, was aber gar nicht zur Fragestellung gehört. Wenn man nun die Geschwindigkeit gegen die Zeit abträgt, wird klar, dass v(t) die Gestalt exp(-t) besitzen muss, da die Geschwindigkeit bei jeder Entfernung s den Wert 100 - s besitzt. Da die Fahrtstrecke zu jedem Zeitpunkt t gerade dem Zeitintegral über v(t) entspricht, das die Form 100 * exp(-x) besitzt, kann man 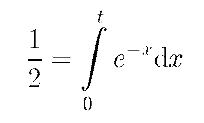
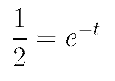
So nett eine analystische Lösung ist, wäre doch ein analoges Modell des Problems noch wesentlich netter. :-) Was also benötigt wird, ist eine Rechenschaltung zu obigem Problem. Wenn wir ein skaliertes Problem unterstellen, bei dem 100 km durch den Wert 1 repräsentiert werden, ergibt sich v(t) = 1 - s(t), wobei s(t) gerade dem Zeitintegral über v(t) entspricht. Die Rechenschaltung ist ausgesprochen einfach: 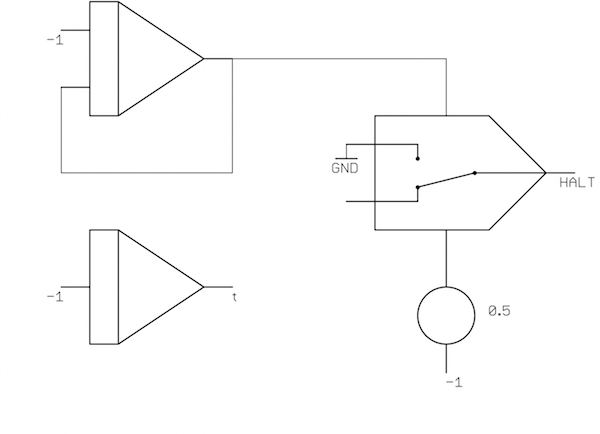
Der untere Integrierer liefert das Zeitintegral über -1, so dass an seinem Ausgang direkt die benötigte Fahrzeit in Stunden abgelesen werden kann. (Verwendet wurde übrigens ein Analogrechner des Typs Telefunken RA 742.)

Als Zeitspanne ergibt sich (mit einem Digitalvoltmeter ist natürlich eine deutlich höhere Ablesegenauigkeit möglich) 
|
|
|
20-JUl-2008, 21-DEC-2008, 19-FEB-2016, ulmann@analogmuseum.org |
